The impact of exercise on gene regulation in association with complex trait genetics
This study did not generate novel data, instead relying on data published in previous or concurrent studies. Animal procedures from the concurrent MoTrPAC PASS1B study4 were approved by the University of Iowa’s Institutional Animal Care and Use Committee.
MoTrPAC EET study design
The MoTrPAC42 Endurance Exercise Training Study is described in detail in the landscape manuscript4 (data accessible at https://motrpac-data.org/data-access). In brief, both female and male F344 rats were subjected to treadmill exercise training, with tissues harvested at 1, 2, 4, and 8 weeks of training. All samples were taken 48 h after the last exercise bout, with the 8-week time point taken to correspond to the adapted state. In this work, we leverage data from a total of 738 extracted samples across 15 tissues and 47-50 rats per tissue that were subjected to RNA-sequencing and differential expression analysis.
Differential expression analysis
Differential expression analysis (DEA) is described in detail by the main MoTrPAC manuscript4. Briefly, DEA was performed separately in each sex and tissue using filtered raw counts as input for DESeq243. Likelihood ratio tests (DESeq2::nbinomLRT()) were used to identify genes that changed over the training time course in at least one sex while accounting for RNA-Seq technical covariates (RNA integrity number, median 5′-3′ bias, percent of reads mapping to globin, and percent of PCR duplicates as quantified with Unique Molecular Identifiers). For each gene, male- and female-specific p-values were combined using the Fisher’s sum of logs method. These meta-analytic p-values were adjusted across all RNA-Seq datasets using Independent Hypothesis Weighting (IHW) with tissue as a covariate44. Training-differential genes were selected at 5% IHW α. Given the regression model of each gene described above, contrasts were made between each training timepoint (i.e., 1, 2, 4, or 8 weeks) and the sex-matched sedentary controls using DESeq2::DESeq() to calculate time- and sex-specific summary statistics.
Correlation of differential analysis results
The nominal p-values and log fold-changes from the time- and sex-specific differential expression analysis results were transformed into standard normal random variables using qnorm(p-value / 2, lower.tail = F) * sign\(({\log }_{2}{{{{{{{\rm{FC}}}}}}}})\) in base-R. These “z-scores" were organized into a gene-by-condition matrix, where conditions were tissue, sex, and timepoint combinations. The z-score matrix was filtered to include the set of genes that had no missing values across all conditions. We calculated the Spearman correlation between all pairs of conditions to quantify the concordance of the training effect across conditions.
Graphical clustering of differential analysis results
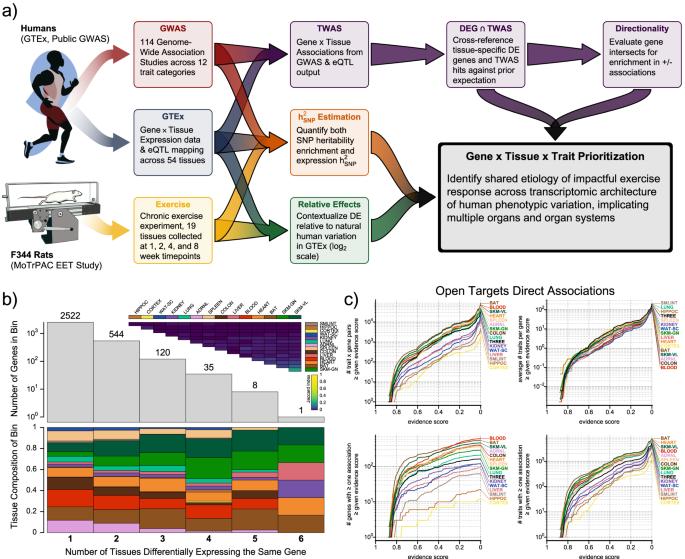
Graphical clustering of differential analysis results is described in detail in the main MoTrPAC EET study manuscript4. All training-differential features at 5% IHW α were clustered into homogeneous patterns using their time- and sex-specific differential analysis z-scores. The statistical details are provided elsewhere4,45,46,47. Briefly, the expectation-maximization (EM) process of the repfdr algorithm was used to assign one of three simplified states to each z-score: −1 for down-regulation, 0 for null (no change), or 1 for up-regulation45. For each feature and timepoint, the simplified states from each sex were combined into one of nine possible states (−1, 0, or 1 for each sex). For example, the state “F1_M1" represented a feature that was up-regulated in both females (F1) and males (M1) at a given timepoint. Here, to focus on genes with sex-consistent training effects in the trained state, we selected genes that were assigned to the F1_M1 state (up-regulated in both sexes) or the F-1_M-1 state (down-regulated in both sexes) at 8 weeks. To enable comparison between genes expressed in rats and humans, we compiled a MoTrPAC rat-to-human ortholog map from GENCODE and RGD resources4,48,49. The distribution of those genes able to be matched to human orthologs across tissues is summarized in Fig. 1b.
Open targets intersection
The Open Targets50 database (Release 22.04) was downloaded on June 8th, 2022. Entries in this database represent curated sets of human genes with disease relationships established from multiple sources of evidence. We used the R-package sparklyr51 to cross-reference differentially expressed rat genes to all orthologous Open Targets gene-trait direct associations at different evidence-score thresholds. The abundance of these associations were quantified on a tissue-specific and tissue-shared bases, comprising genes differentially expressed in three or more tissues. A table listing all genes, top trait associations, and corresponding tissues is provided in the Supplementary Files folder of the GitHub repo.
Heritability analyses
We retrieved summary statistics (sumstats) for 114 published GWAS5. Using the program LDSC9, we estimated SNP-heritability (\({h}_{{{{{{{{\rm{SNP}}}}}}}}}^{2}\)) for each GWAS in LDSC10, including the default baseline annotation of 53 functional categories. We further estimated \({h}_{{{{{{{{\rm{SNP}}}}}}}}}^{2}\) using MESC11, and with the provided expression scores meta-analyzed over 48 GTEx tissues, estimated expression-mediated heritability (\({h}_{{{{{{{{\rm{mediated}}}}}}}}}^{2}\)) for our 114 traits, as well as the ratio of \({h}_{{{{{{{{\rm{mediated}}}}}}}}}^{2}/{h}_{{{{{{{{\rm{SNP}}}}}}}}}^{2}\).
LDSC was used to estimate overall proportion of and enrichment in \({h}_{{{{{{{{\rm{SNP}}}}}}}}}^{2}\) across loci within a 100kb window of all sex-consistent 8w DE gene sets in each tissue following the “Cell type specific analyses" tutorial. We included here the baseline annotation, as well as an annotation comprising loci within 100kb of all expressed genes in each tissue. Finally, to assess the sensitivity of tissue-specific results on overlaps in gene sets between tissues, we estimated heritability and heritability enrichment conditional on annotations corresponding to all other tissues alongside the baseline annotation.
Human expression data & effect standardization
To assess the degree that exercise effects could overcome genetic and phenotypic variability of gene expression in a tissue, we used the GTEx database (version 8)34. To allow for a common scale between exercise DE and measures of gene expression in GTEx, we modified the GTEx pipeline to use a pseudolog (log2(x + 1)) transformation in place of its default inverse-normal transform, otherwise keeping later steps in the pipeline intact. Next, we took the outputted expression matrices and residualized out the provided covariates using the lm() function in base-R (sex, the top 5 genotyping principal components, Sequencing platform, Sequencing protocol, and the suggested number of PEER factors in the GTEx documentation). On a per-gene basis, we then computed sample variances for each gene in each tissue, pooled across sex to reflect the sex-independent nature of exercise-induced DE. To regularize outlying variance estimates due to sampling effects, we fit an inverse-gamma distribution to tissue-specific sample variances using a maximum goodness-of-fit estimator implemented in the R-package fitdistrplus52 by the function fitdist(). As the inverse-gamma is the conjugate prior of the variance term of a normal distribution with known mean, we adopted an Empirical Bayesian strategy to produce posterior estimates of each gene’s expression variance. To allow for heterogeneity in this term across sex, we did this separately for male- and female-coded individuals in the GTEx study population. Additional details are provided in the Supplementary Methods. Across tissues, these empirical priors are plotted in the denominator of Fig. 2a. For each gene, we then took the square root of the posterior mean of inferred log2expression variance (\(\sqrt{\,{{\mbox{Var}}}\,({\log }_{2}({{{{{{{\rm{gene}}}}}}}}\,{{{{{{{\rm{expression}}}}}}}}))}\)) to estimate within-population standard deviation of the magnitude of gene expression. We then divided estimated exercise DE by these values to produce standardized estimates in units of within-tissue phenotypic standard deviation (SDpheno). Further, these estimates were conditioned on both sex and population (quantile plots in upper panels of Fig. 2a).
To estimate the scale of genetic influence on gene expression, we used the software Plink53 and GCTA54, specifically GCTA-GRM55, to estimate \({h}_{{{{{{{{\rm{SNP}}}}}}}}}^{2}\) of each gene’s expression, using the same covariates as before. In contrast to prior work estimating \({h}_{{{{{{{{\rm{SNP}}}}}}}}}^{2}\) in GTEx’ inverse-normal transformed gene expression matrices56, we focused on obtaining estimates on a gene-specific basis, and so constrained output to be bounded between 0 and 1.
We then took these estimates, which represent the proportion of expression variance able to be explained by linear effects at the SNP level, and multiplied them by the estimates of expression variance, dividing our estimates of exercise-induced DE by the square root of that product to obtain exercise-effect sizes in units of genetic (SNP) standard deviation (SDgeno). Many of these \({h}_{{{{{{{{\rm{SNP}}}}}}}}}^{2}\) point estimates were at or near 0, resulting in extreme standardized effect sizes. As a further filter, we thresholded on significance (IHW α = 0.10, with tissue as a covariate) to focus on confidently heritable genetically regulated expression. This removed ≈92% of gene x tissue pairs (583,238/632,738), leaving 49,500 for later analysis and use in figures.
Cross-referencing exercise-training genes with human TWAS
To identify specific genes where exercise-training effects may have the potential to mediate traits, we cross-referenced exercise-genes against transcriptome-wide association results (TWAS). Specifically, we downloaded S-PrediXcan13 output5 for 114 GWAS and MASHR-based expression models using GTEx v8, filtering by significance (IHW α = 0.05, with tissue x trait pairs as a covariate), and intersected with genes that were differentially expressed due to exercise at 8W in a sex-consistent manner, i.e., members of the nodes “8w_F1_M1" and “8w_F-1_M-1". 99 of 114 traits had a nonzero intersect in at least one tissue.
To assess potential enrichments in these intersections, we compared the observed count of S-PrediXcan hits in the DEG sets against those outside the DEG sets, adopting a tractable Binomial approximation to the Bernoulli distribution to test for enrichment or depletion of genes under a multilevel Bayesian model, following ref. 57. This approach allowed us to partially pool information across tissues and traits, avoiding the need for post-hoc multiplicity adjustment58, as multiplicity is explicitly built into the inference model itself through flexible regularization of model parameters towards 0. Specifically, we fit a model of the form:
$${y}_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}} \sim \,{{\mbox{Binomial}}}\,({n}_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}},\, f({\pi }_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}}))$$
(1.1)
$${y}_{{{{{{{{\rm{i,j}}}}}}}}}^{\neg \,{{\mbox{DEG}}}} \sim {{\mbox{Binomial}}}\,({n}_{{{{{{{{\rm{i,j}}}}}}}}}^{\neg \,{{\mbox{DEG}}}\,},\, f({\pi }_{{{{{{{{\rm{i,j}}}}}}}}}^{\neg \,{{\mbox{DEG}}}\,}))$$
(1.2)
$${\pi }_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}}={\pi }_{{{{{{{{\rm{i,j}}}}}}}}}+\frac{\alpha+{\beta }_{{{{{{{{\rm{i}}}}}}}}}+{\gamma }_{{{{{{{{\rm{j}}}}}}}}}+{\epsilon }_{{{{{{{{\rm{i,j}}}}}}}}}}{2}$$
(1.3)
$${\pi }_{{{{{{{{\rm{i,j}}}}}}}}}^{\neg \,{{\mbox{DEG}}}\,}={\pi }_{{{{{{{{\rm{i,j}}}}}}}}}-\frac{\alpha+{\beta }_{{{{{{{{\rm{i}}}}}}}}}+{\gamma }_{{{{{{{{\rm{j}}}}}}}}}+{\epsilon }_{{{{{{{{\rm{i,j}}}}}}}}}}{2}$$
(1.4)
$$\alpha \sim \,{{\mbox{Normal}}}\,(0,\, 1)$$
(1.5)
$${\beta }_{{{{{{{{\rm{i}}}}}}}}} \sim \,{{\mbox{Multi-Normal}}}\,(\overrightarrow{{{{{{{{\bf{0}}}}}}}}},\, {\sigma }_{\beta }^{2}{\Sigma }_{{{{{{{{\rm{i}}}}}}}}})$$
(1.6)
$${\gamma }_{{{{{{{{\rm{j}}}}}}}}} \sim \,{{\mbox{Multi-Normal}}}\,({\overrightarrow{{{{{{{{\mathbf{\mu }}}}}}}}}}_{{{{{{{{\rm{k}}}}}}}}},\, {\sigma }_{\gamma }^{2}{\Sigma }_{{{{{{{{\rm{j}}}}}}}}})$$
(1.7)
$${\epsilon }_{{{{{{{{\rm{i,j}}}}}}}}} \sim \,{{\mbox{Multi-Normal}}}\,(\overrightarrow{{{{{{{{\bf{0}}}}}}}}},\, {\sigma }_{\epsilon }{\Sigma }_{{{{{{{{\rm{i}}}}}}}}\times {{\mbox{j}}}})$$
(1.8)
$${\mu }_{{{{{{{{\rm{k}}}}}}}}} \sim \,{{\mbox{Normal}}}\,(0,\, {\sigma }_{\mu })$$
(1.9)
$${\pi }_{{{{{{{{\rm{i,j}}}}}}}}} \sim \,{{\mbox{Multi-Normal}}}\,({\eta }_{{{{{{{{\rm{j}}}}}}}}},\, {\sigma }_{\pi }{\Sigma }_{{{{{{{{\rm{i}}}}}}}}\times {{\mbox{j}}}})$$
(1.10)
$${\eta }_{{{{{{{{\rm{j}}}}}}}}} \sim \,{{\mbox{Multi-Normal}}}\,({\overrightarrow{{{{{{{{\mathbf{\lambda }}}}}}}}}}_{{{{{{{{\rm{k}}}}}}}}},\, {\sigma }_{\eta }^{2}{\Sigma }_{{{{{{{{\rm{j}}}}}}}}})$$
(1.11)
$${\lambda }_{{{{{{{{\rm{k}}}}}}}}} \sim \,{{\mbox{Normal}}}\,(\mu,\, {\sigma }_{\lambda })$$
(1.12)
$$\mu \sim \,{{\mbox{Normal}}}\,(0,\, 2)$$
(1.13)
$${\sigma }_{\beta,\gamma,\epsilon,\mu,\pi,\eta,\lambda } \sim \,{{\mbox{Half-Normal}}}\,(0,\, 1)$$
(1.14)
Notation for this model is summarized in Supplementary Table 2, but in brief: the intersect size \({y}_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}}\) in tissue i ∈ {1, 2, …, 15} and trait j ∈ {1, 2, …, 99} was binomially distributed, with \({n}_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}}\) giving the total number of genes in that tissue that were differentially expressed at 8W and expressed at any level in the PrediXcan analysis (i.e., disregarding genes that were not expressed in both samples). The function f() can be any function mapping \({\mathbb{R}}\to (0,1)\), but here was the inverse-logit function. On the logit-scale, \({\pi }_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}}\) was expressed as a deviation from a mean πi,j, with an equal and opposite deviation to the log-odds of observing a PrediXcan hit in the complementary set, defined as all expressed genes that were not differentially expressed at 8W in a sex-consistent manner. This deviation term had four components: a tissue difference βi, a trait difference γj, a tissue x trait difference ϵi,j, and an overall difference α. Adding and subtracting half from πi,j to produce \({\pi }_{{{{{{{{\rm{i,j}}}}}}}}}^{{{{{{{{\rm{DEG}}}}}}}}}\) and \({\pi }_{{{{{{{{\rm{i,j}}}}}}}}}^{\neg \,{{\mbox{DEG}}}\,}\), respectively, was done to prevent specifying greater prior uncertainty on one of the two composite probability parameters.
The various scale parameters, σ, served to adaptively regularize estimates of each difference term towards their mean. Otherwise, we nested trait difference effects γj in trait category difference effects μk, where k ∈ {1, 2, …, 12} indexes previously designated trait categories5, i.e., members of the set {Psychiatric, Aging, Cardiometabolic, Allergy, Digestive, Immune, Endocrine, Skeletal, Anthropometric, Hair, Blood, Cancer}. If traits in a particular category showed consistent evidence of deviation, partial pooling shrunk estimates towards their respective mean hyperparameters, allowing them to share information to the extent the model could detect information to be shared. We use a similar model structure to express the overall location parameter, πi,j.
Pseudo-replication across tissues and traits amplifies signals that inform higher-level parameters, leading the inference model to mistake interdependent effects as independent evidence for enrichment. When aggregating many Bernoulli random variables to a single binomial, signals of gene interdependence that would otherwise prevent this are lost. To address this, we introduced parameters Σi, Σj, and Σi×j, corresponding to i × i tissue, j × j trait, and (i ⋅ j) × (i ⋅ j) tissue × trait correlation matrices, respectively. For tractability, we then fixed these to maximum-likelihood estimates of each respective gene-wise correlation matrix under a bivariate probit, which we fit marginally across all DEGs, PrediXcan hits (jointly across tissues), and DEG × PrediXcan intersects using the nlm (non-linear minimization) algorithm59 implemented in and accessed through the R-packages stats and optimx60. As we fit each pairwise correlation individually, rather than simultaneously, there was no guarantee that the resulting correlation matrix is positive semi-definite. To ensure this constraint is met and all pairwise correlations are jointly possible, we transformed the pairwise-estimated correlation matrices with Higham’s algorithm61 implemented in the R-package Matrix62 function nearPD() before proceeding further.
We fit this model in Stan63 using CmdStanR64 and in Fig. 4e–g visualize marginal posterior distributions for tissue, trait, and trait category difference effects as violin plots using the R-package vioplot65. Additionally, where the composite difference effect for a particular cell in Fig. 4a finds > 95% of its posterior mass to one side of 0, we colored its upper or lower corner with a red or blue triangle to signify enrichment or depletion of that tissue x trait combination, respectively. To accommodate this and subsequent models’ challenging posterior geometry, we used a non-centered parameterization, running four separate and randomly initialized chains for 2.5 × 103 warmup and 2.5 × 103 sampling iterations, with a target acceptance rate δ of 0.95. To diagnose pathologies in the MCMC output and confirm adequate convergence, mixing, and sampling intensity, we used the posterior package66 for MCMC diagnostics, requiring that all model parameters, as well as posterior density and likelihood, receive \(\hat{r} and both bulk and tail Effective Sample Size (ESS) > 500, in addition to requiring that To complement this analysis, we also performed frequentist Gene Set Enrichment Analysis using the function fgsea() implemented in the R-package fgsea67. Specifically, for each trait × tissue pair, we assessed enrichment of the set of DEGs in that tissue in the list of -log10(p-values) of mutually expressed, orthologous genes’ p-values from PrediXcan, applying a Bonferroni correction to the output. To aggregate across these interdependent tests and assess tissue- and trait-level enrichment, we took the harmonic mean of subtest p-values corresponding to each grouping68, applying a similar FWER adjustment to the output (α = 0.05). We leveraged the same meta-analytic procedure over trait-level enrichments to aggregate to trait categories. Finally, we explored an alternative approach to aggregating multi-tissue GSEA within traits. As a more stringent set of multi-tissue responsive genes, we took the set of all genes differentially expressed in three or more tissues. For PrediXcan p-values, we took the harmonic mean of PrediXcan p-values for each gene across all studied tissues prior to -log10 transformation. These were input into conventional GSEA, and output from all of the above comparisons was visualized in Supplementary Fig. 3. To assess the proportion of DE acting in disease-like directions relative to each phenotype (the product of the direction of DE and the direct of association from PrediXcan), we applied another Bayesian multilevel model, comparing the observed, unweighted frequency of positive effects against a “null" frequency of 0.5 (equivalently, against log-odds of 0): $${y}_{{{{{{{{\rm{i,j}}}}}}}}} \sim \,{{\mbox{Binomial}}}\,({n}_{{{{{{{{\rm{i,j}}}}}}}}},\, f({\pi }_{{{{{{{{\rm{i,j}}}}}}}}}))$$
(2.1)
$${\pi }_{{{{{{{{\rm{i,j}}}}}}}}} \sim \,{{\mbox{Normal}}}\,({\overrightarrow{{{{{{{{\mathbf{\mu }}}}}}}}}}_{{{{{{{{\rm{j}}}}}}}}},\, {\sigma }_{{{{{{{{\rm{j}}}}}}}}})$$
(2.2)
$${\overrightarrow{{{{{{{{\mathbf{\mu }}}}}}}}}}_{{{{{{{{\rm{j}}}}}}}}} \sim \,{{\mbox{Multi-Normal}}}\,(\overrightarrow{{{{{{{{\bf{0}}}}}}}}}\!\!,\, {{{\mbox{SRS}}}}^{{{\mbox{T}}}})$$
(2.3)
$$\,{{\mbox{R}}}={{{\mbox{G}}}}_{{{{{{{{\rm{SNP}}}}}}}}}\times \theta+\,{{\mbox{I}}}\,\times (1-\theta )$$
(2.4)
$$\theta \sim \,{{\mbox{Beta}}}\,(1,\, 1)$$
(2.5)
$$\,{{\mbox{diag}}}({{\mbox{S}}}\,)=\delta {e}^{{\gamma }_{{{{{{{{\rm{k}}}}}}}}}}$$
(2.6)
$${\gamma }_{{{{{{{{\rm{k}}}}}}}}} \sim \,{{\mbox{Normal}}}\,(0,\, {\sigma }_{\gamma })$$
(2.7)
$${\sigma }_{{{{{{{{\rm{j}}}}}}}}}=\rho {e}^{{\lambda }_{{{{{{{{\rm{j}}}}}}}}}}$$
(2.8)
$${\lambda }_{{{{{{{{\rm{j}}}}}}}}} \sim \,{{\mbox{Normal}}}\,(0,\, {\sigma }_{\lambda })$$
(2.9)
$$\rho,\, \delta \sim \,{{\mbox{Half-Normal}}}\,(0,\, 2)$$
(2.10)
$${\sigma }_{\gamma,\lambda } \sim \,{{\mbox{Half-Normal}}}\,(0,\, 1)$$
(2.11)
Unlike for their overall frequency, signal for the directionality of effect (more or less disease-like) cannot be shared across traits or within trait categories, as the traits themselves vary in whether they are harmful, neutral, or beneficial. Instead, we perform partial pooling across the scale of these differences, across both trait categories and within traits themselves. Notation for this model is summarized in Supplementary Table 3, but in brief: we estimate overall scale parameters (ρ, δ), and then estimate a log-normally distributed multiplicative factor (λj, γk) to scale each on a trait-wise and trait-category-wise basis, respectively. To accommodate per-trait interdependence in the direction of deviation, we invert Cheverud’s conjecture69, using our previously estimated GSNP as a proxy for an environmental correlation matrix (Supplementary Fig. 1a). As these genetic correlations were estimated pairwise, positive-semidefiniteness (PSD) of the whole correlation matrix is not guaranteed. To satisfy the PSD constraint of GSNP, we substituted the nearest PSD correlation matrix output from Higham’s algorithm61, implemented in the R-package Matrix62 function nearPD(). To allow flexibility in this modeling assumption, we compute a linearly weighted average of this matrix and the identity matrix (i), estimating the weight parameter θ from a flat Beta prior. MCMC sampling parameters were specified and diagnostics performed as previously described. We examined the two non-anthropometric traits with the highest posterior means in Fig. 6, tracing the proportion of effects of the 8W gene set backwards to the first week. Where individual genes are not assigned to a graphical node signifying differential expression, their contribution to the count of positive effects was taken to be 0.5 when calculating the overall proportion. We include in these tissue-specific trajectories the set of genes corresponding to each tissue, their direction of effect on the trait, and their standardized effect size from Fig. 2b. Similar figures to Fig. 6 for all other traits may be found in the GitHub repository mentioned below. Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.Proportion of disease-like effects
Reporting summary


 Australia
Australia Argentina
Argentina  Austria
Austria  Brazil
Brazil  Canada
Canada  Germany
Germany  Ireland
Ireland  Italy
Italy  Malaysia
Malaysia  Mexico
Mexico  New Zealand
New Zealand  Poland
Poland  South Africa
South Africa  United Kingdom
United Kingdom  United States
United States